Lecture 9
Visualizing relationships with networks, graphs and trees
Georgetown University
Spring 2024
Agenda and Goals for Today
Lecture
Lab
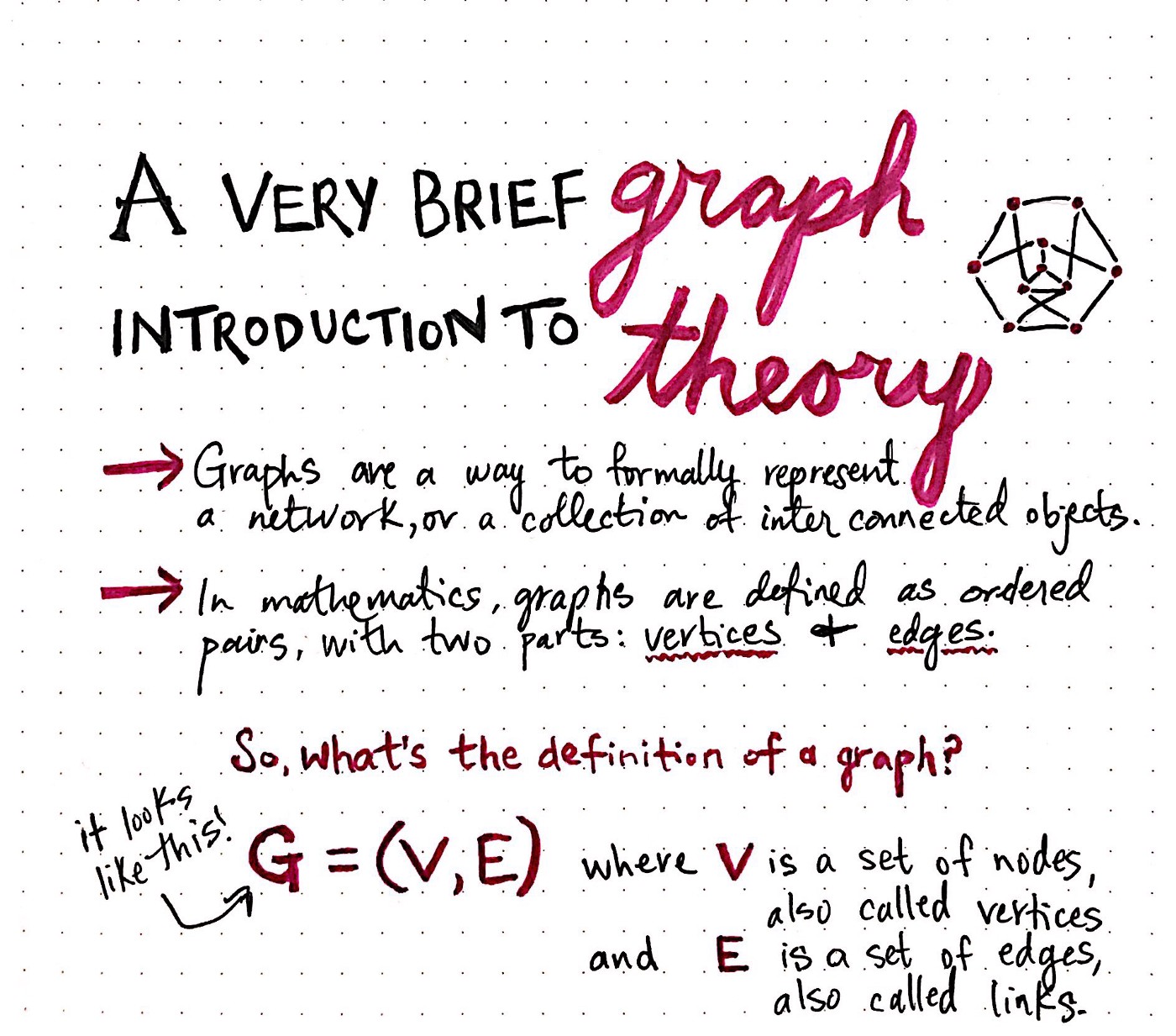
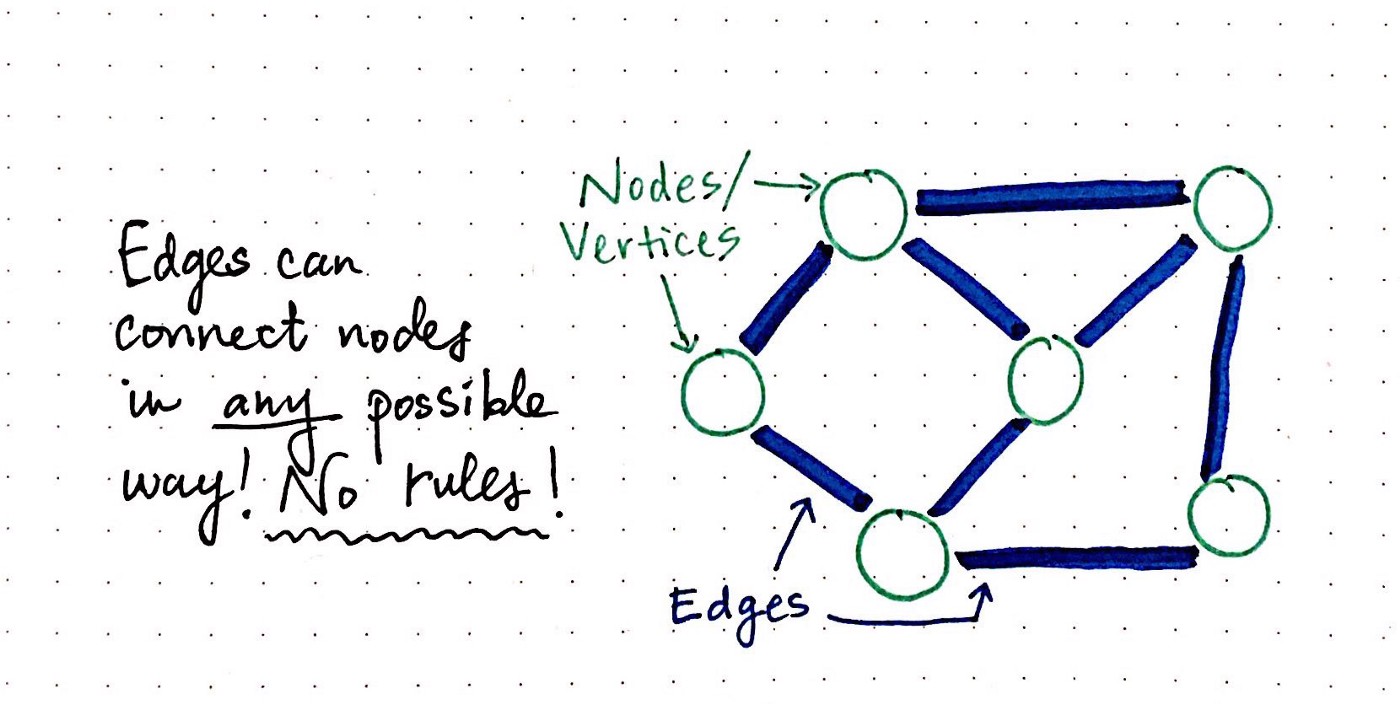
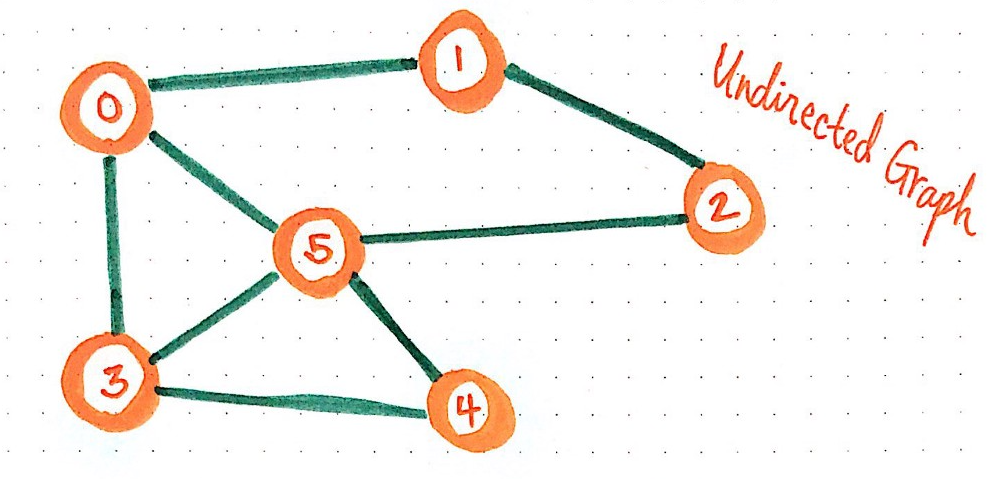
Graph theory review
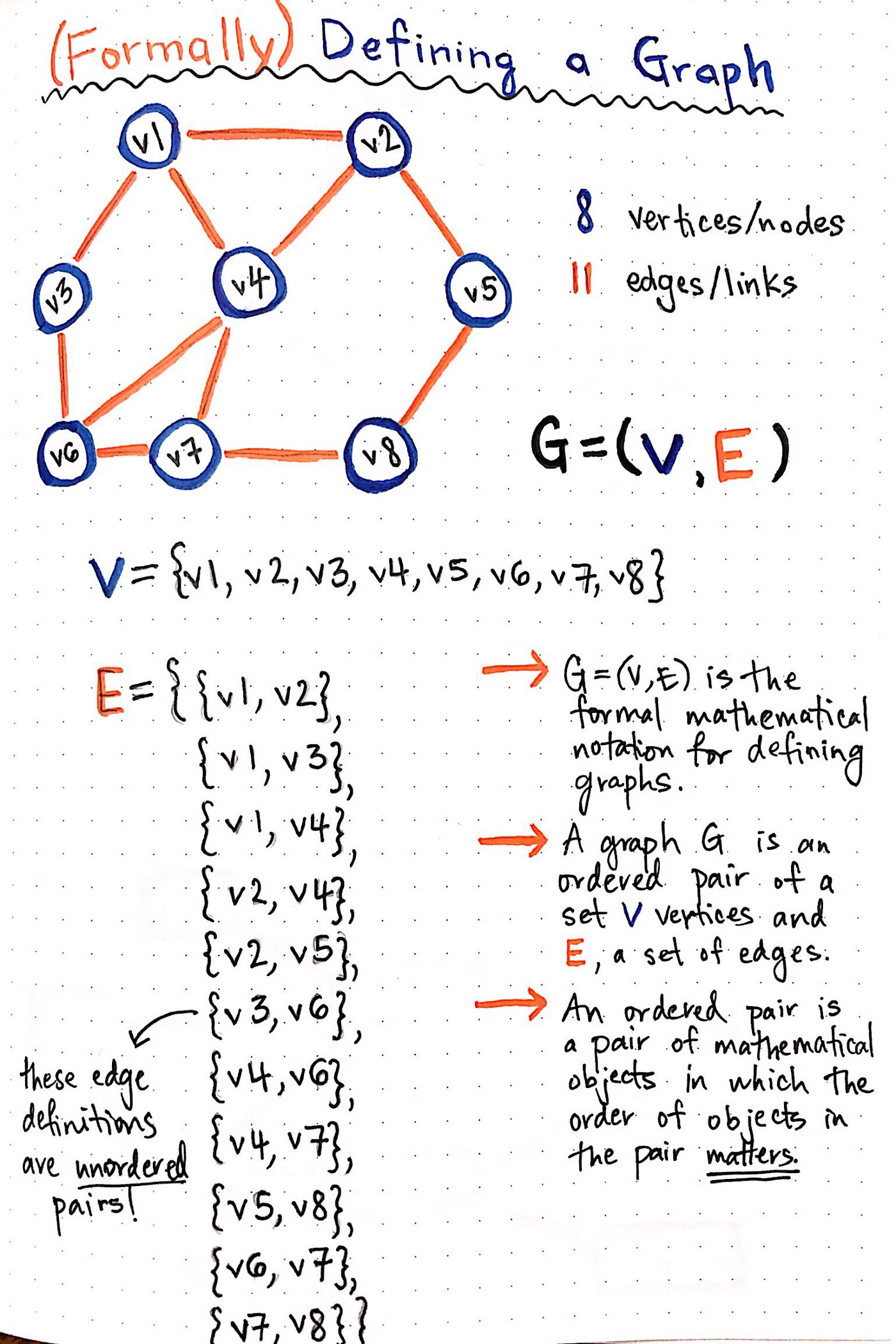
Ways to express a graph
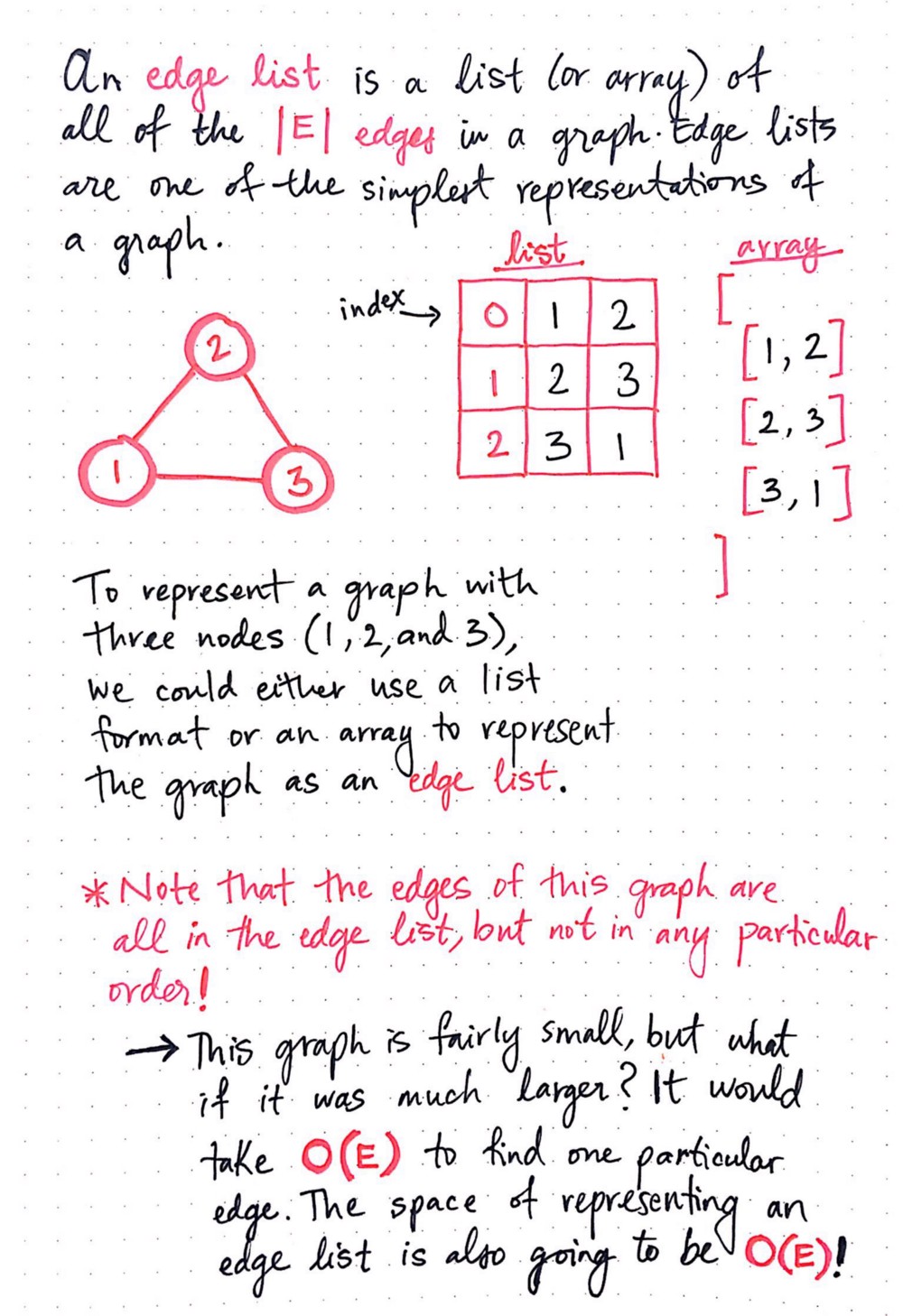
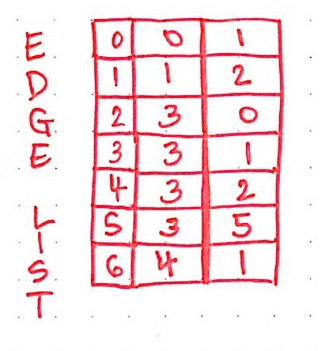
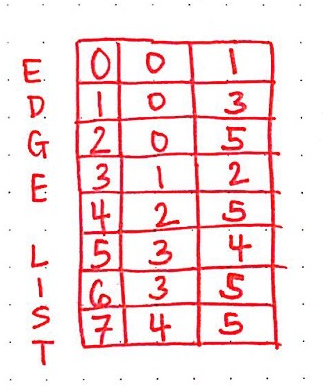
Edge List
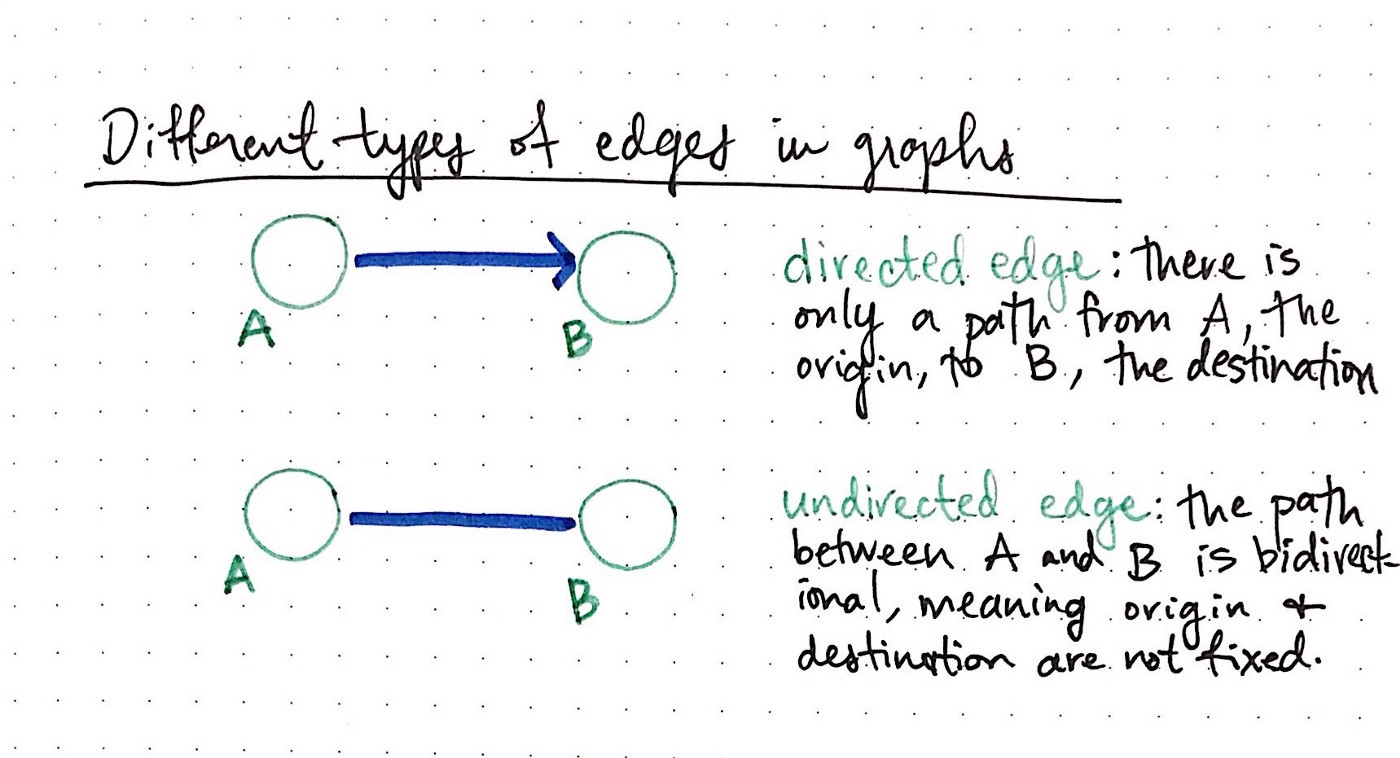
Edge Types
Adjacency Matrix
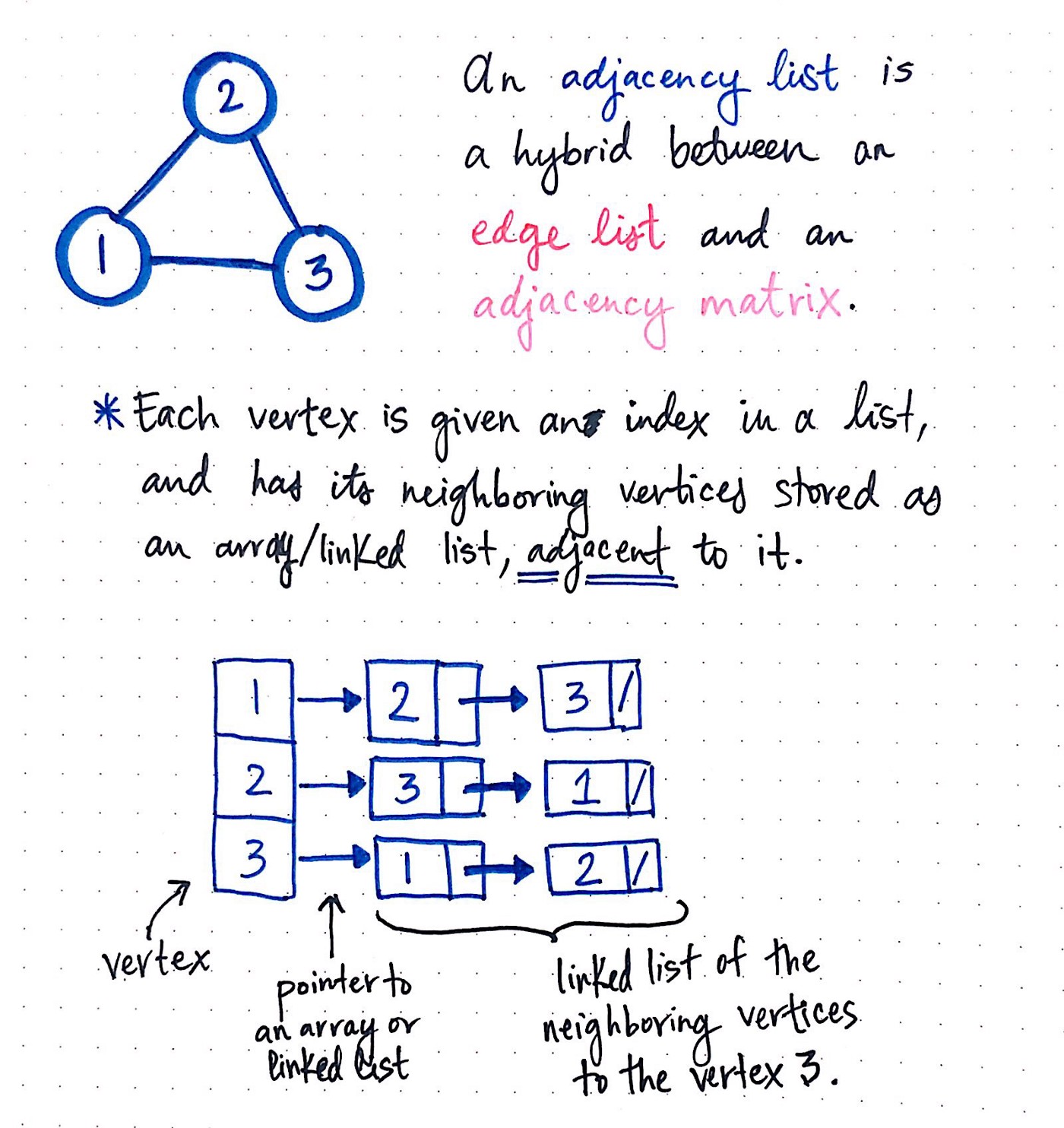
Adjacency List
Caution!
What do you need to fully represent a graph?
Directed Edge List
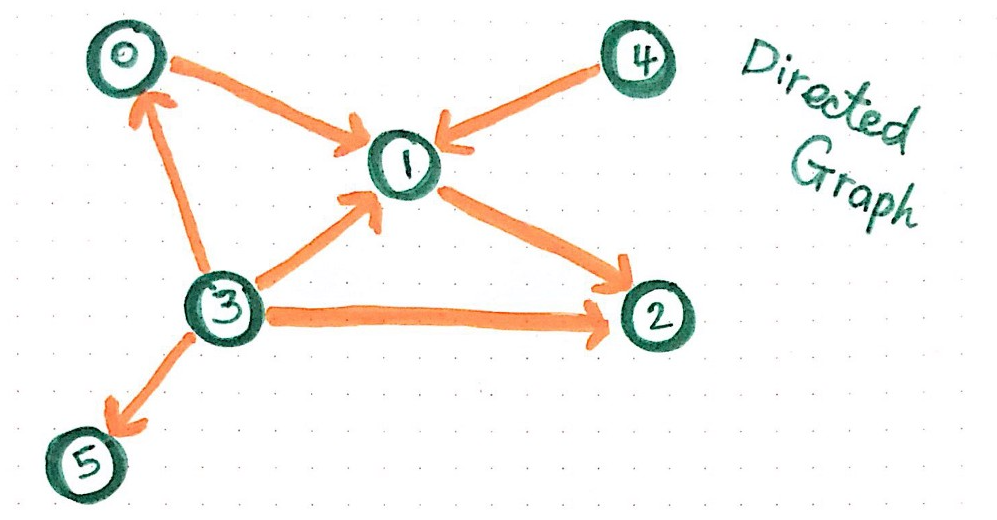
Directed Adjacency Matrix
Directed Adjacency List
Undirected Edge List
Undirected Adjacency Matrix
Undirected Adjacency List
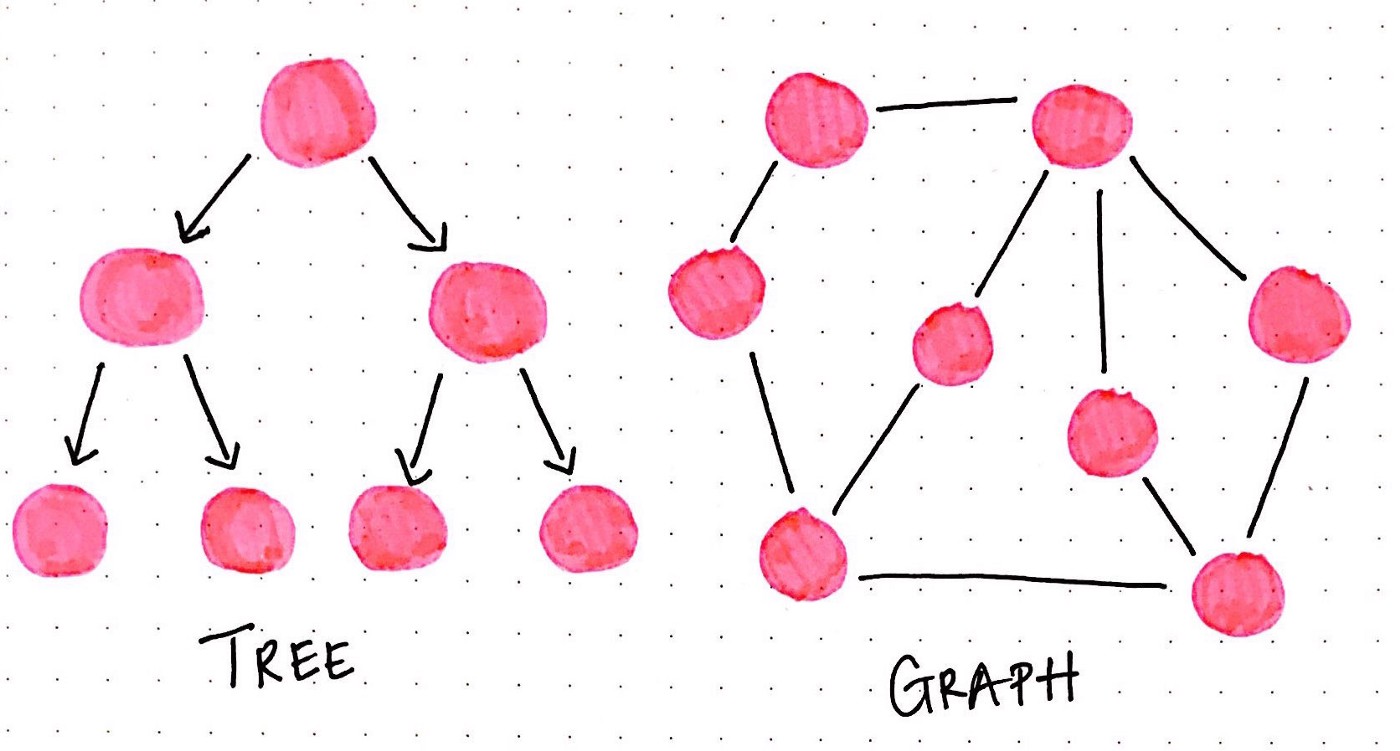
Trees vs. Graphs
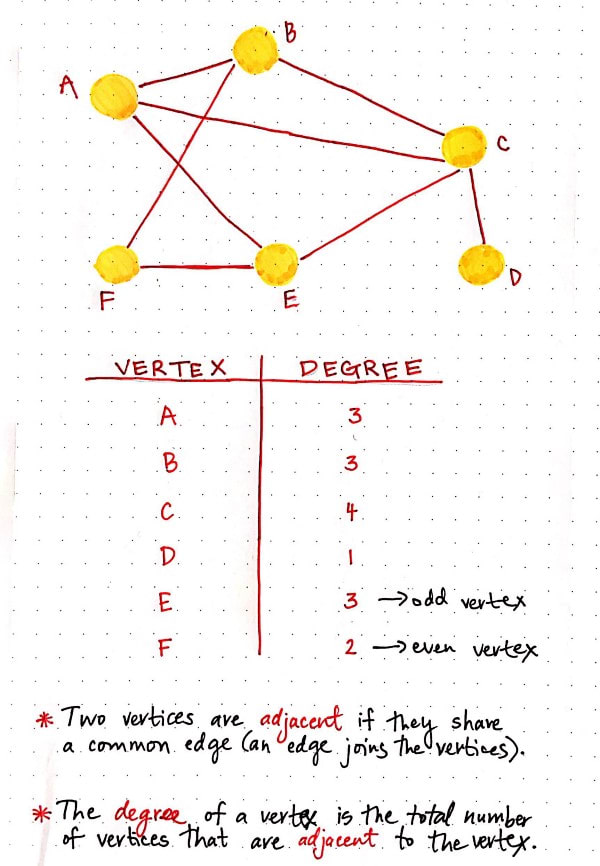
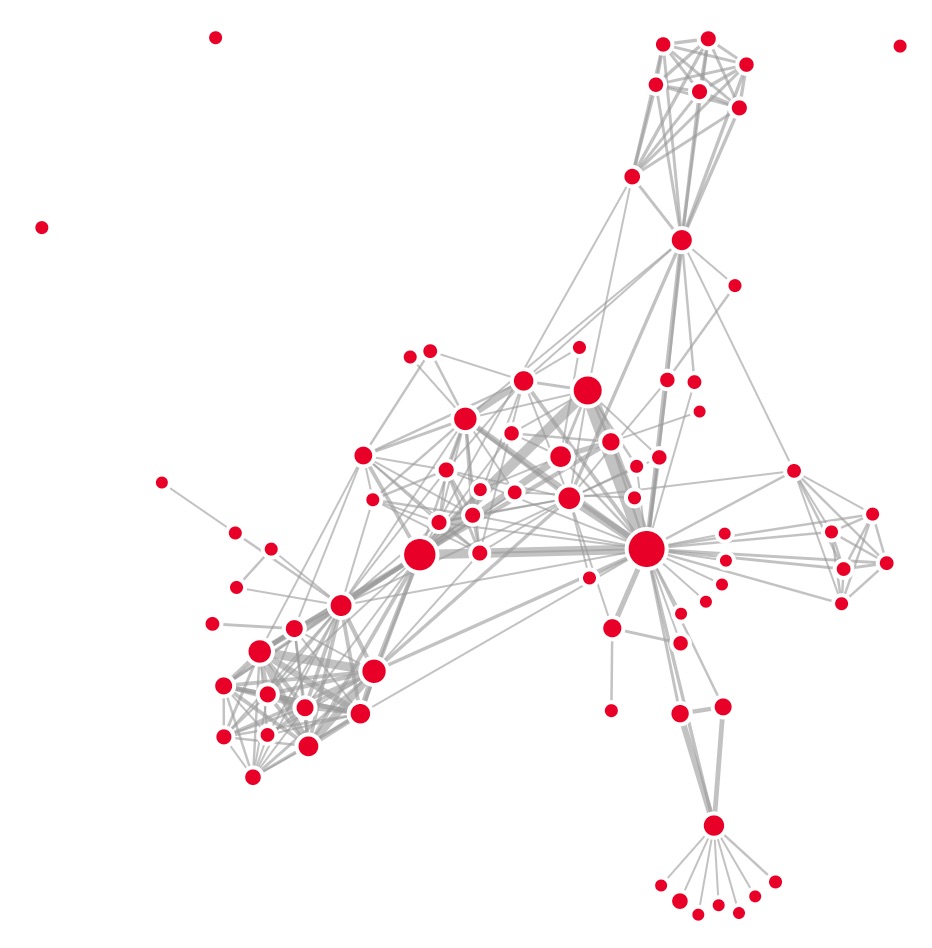
Some important and useful graph measurements
Node measurements
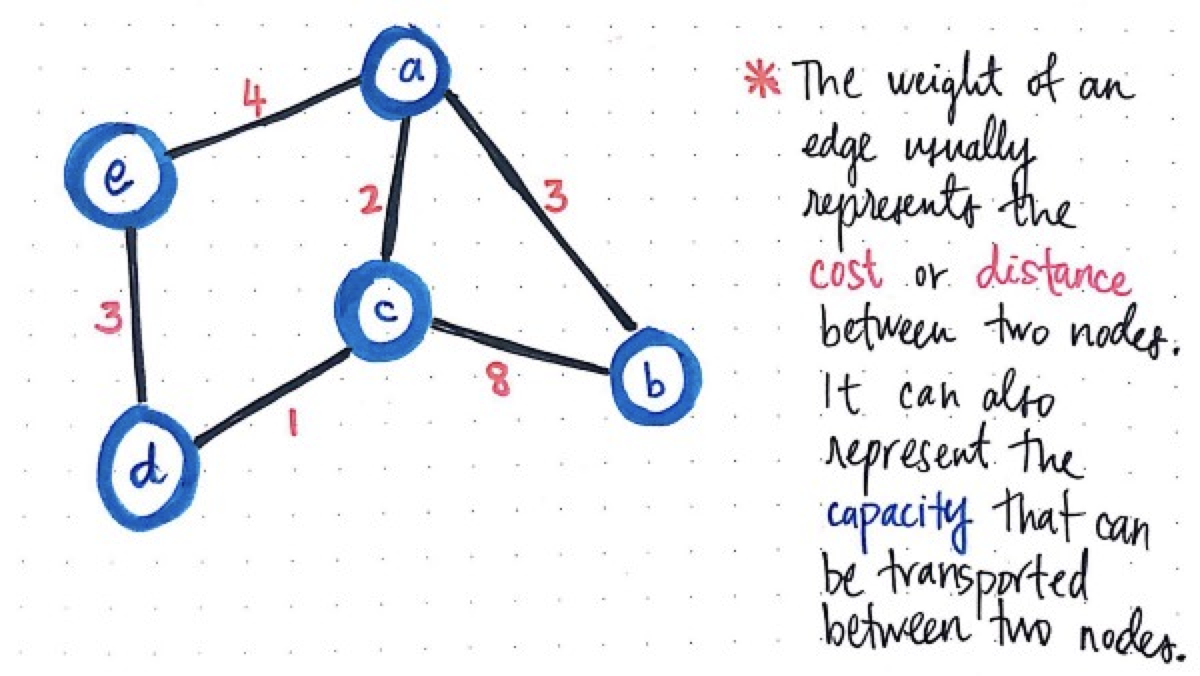
Edge weigths
Various centrality measures
Prepping your data for graphs
Packages for working with and visualizing graphs
Prepping data, graph/network analysis * tidygraph * igraph
Network analysis specific * sna * network
Visualizing * ggraph * igraph * networkD3
Building your graph dataset
The best practice for building an visualizing a graph is to have two tabular datasets representing nodes and edges. Both are needed to represent a complete graph!
An edge list (dataframe) where the first two columns are from and to (required) and the values are the id of the nodes. You can have more fields in the edge list representing additional attributes of your edges.
In a directed graph the from and the to matter. In an undirected graph the order does not matter.
In graphs with multiple edges between nodes, you can set up the edge list in the following ways: * An individual record per edge * One record per unique edge with aggregated data for the edge
A node/vertex list (dataframe) where you have one record per every node (even if they don’t have edges) and the first column is id which represents a unique id for the node. This id value is the same one that is utilized in the edge list.
Your dataframe can also have more columns with different attributes for the node.
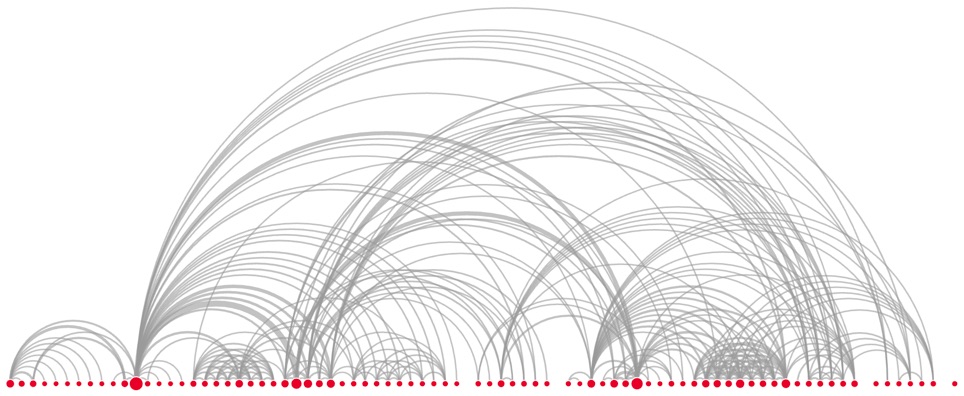
Layouts
There are many positioning algorithms
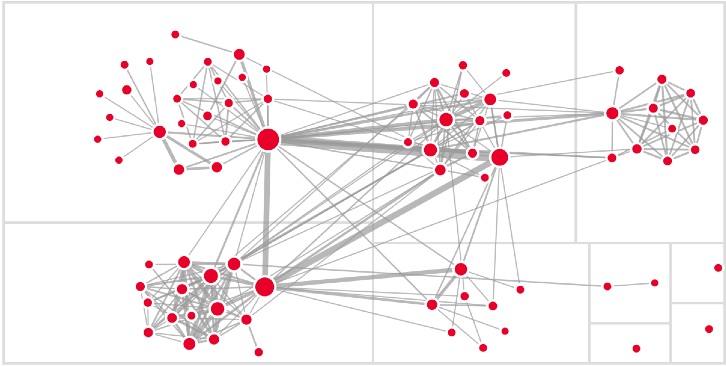
Arc Diagram
Grouped Clusters
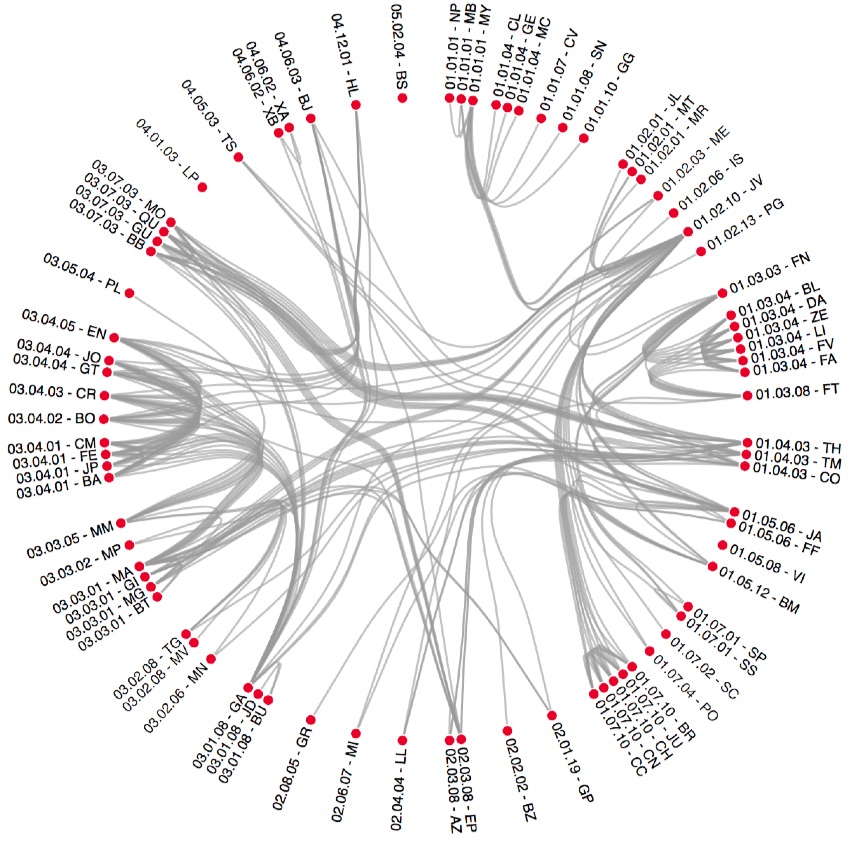
Chord or Radial
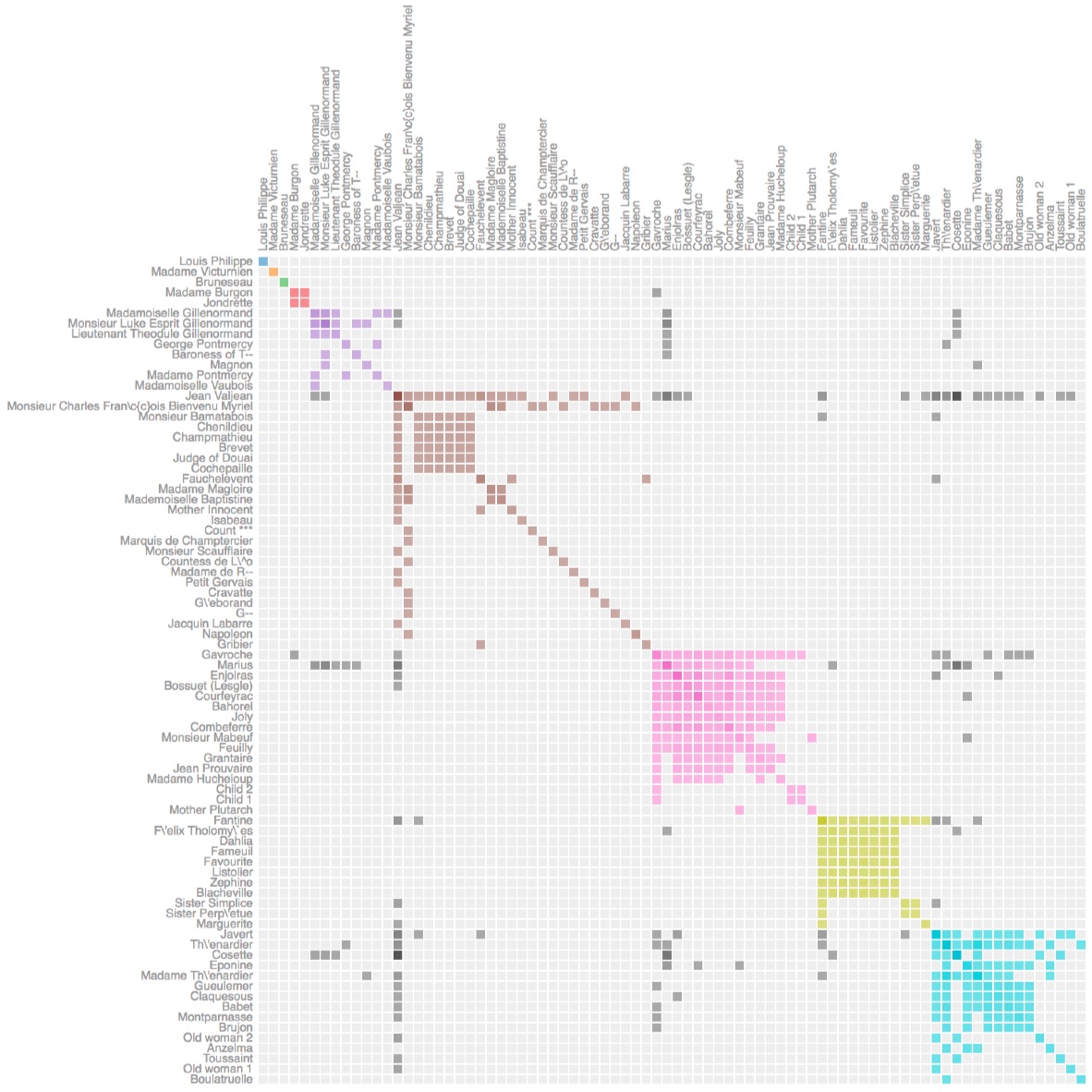
Visual Matrix (representing adjacency matrix)
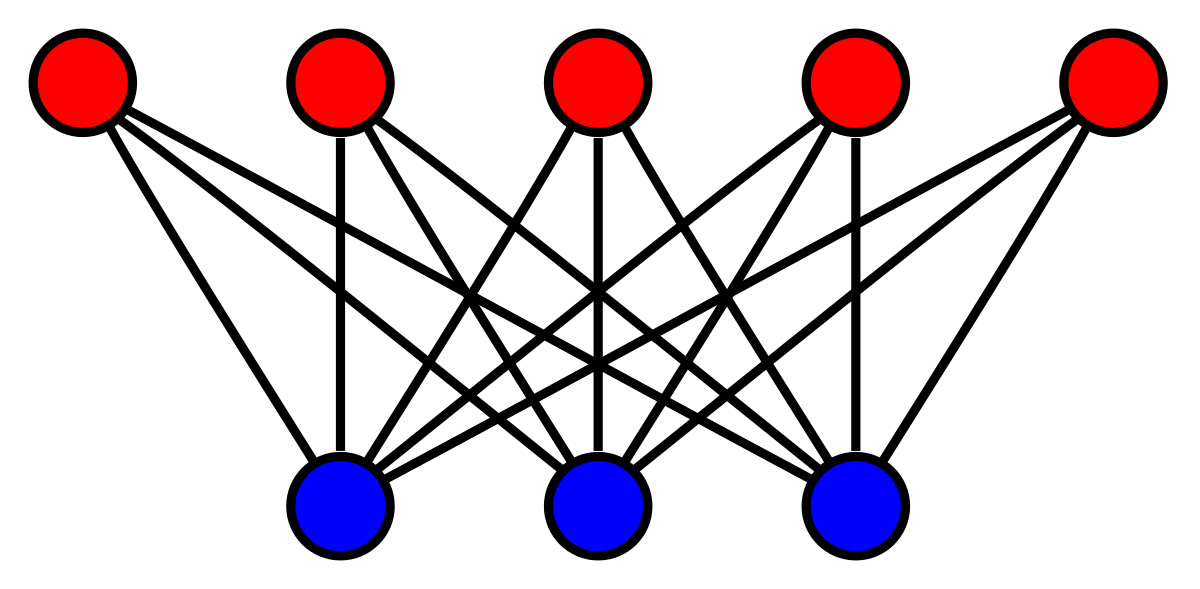
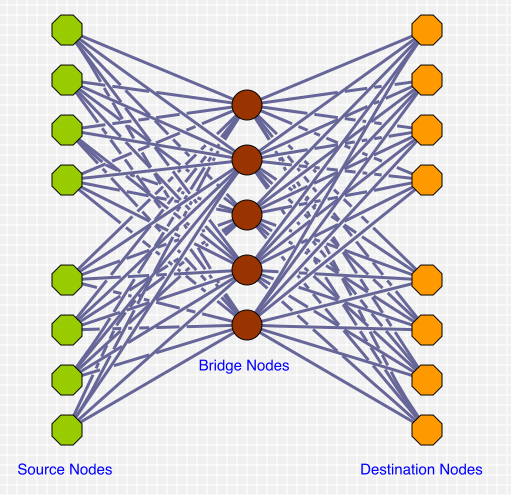
Multimodal graphs
Examples
References & Examples
R
- Katya Ognyanova static & dynamic network viz with R (
igraph) - RStudio
tidygraphexamples - Network Analysis
- NetworkD3 example
Some cool networks examples using Observable
https://johnguerra.co/lectures/information_visualization_spring2023/08_Networks_and_Color/#/3
Trees
Trees are a special kind of network.
https://johnguerra.co/lectures/information_visualization_spring2023/09_Trees_and_Geo/#/2/1
DSAN 5200 | Spring 2024 | https://gu-dsan.github.io/5200-spring-2024/